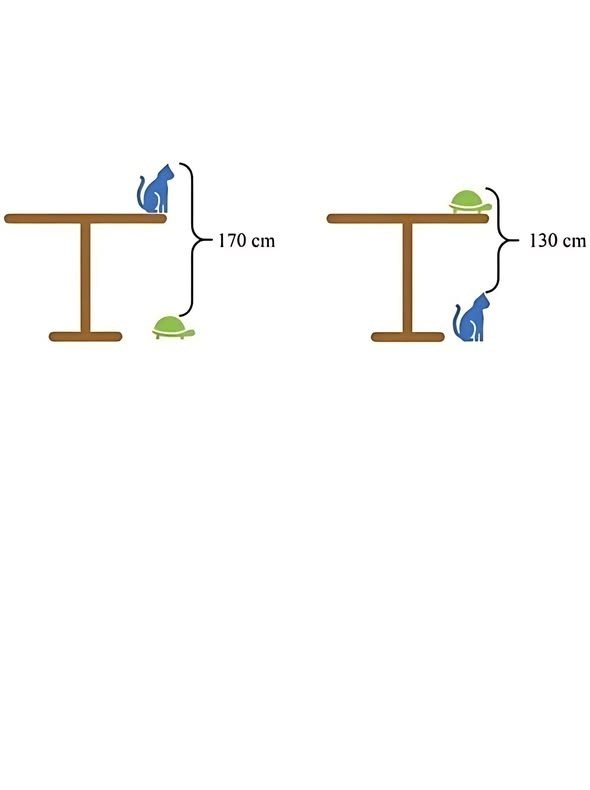
Manchmal wirkt ein Rätsel einfach, bis man versucht, es zu lösen. Die Abbildung mit einer Katze, einer Schildkröte und einem Tisch ist so ein klassisches Beispiel. Es werden zwei Messungen gegeben: eine, wenn die Katze auf dem Tisch sitzt und die Schildkröte auf dem Boden, und eine, wenn ihre Positionen vertauscht sind. Die Frage ist einfach: Wie hoch ist der Tisch?
Die Abbildung zeigt zwei Situationen:
Katze auf dem Tisch, Schildkröte auf dem Boden: Der Höhenunterschied beträgt 170 cm.
Schildkröte auf dem Tisch, Katze auf dem Boden: Der Höhenunterschied beträgt 130 cm.
Es wirkt vielleicht kompliziert, aber mit ein wenig logischem Denken findet man die Lösung schnell.
Die Variablen
Lassen wir es ordentlich aufschreiben:
T = Höhe des Tisches
C = Höhe der Katze
U = Höhe der Schildkröte
Aus der ersten Situation folgt:
(T + C) – U = 170
Aus der zweiten Situation folgt:
(T + U) – C = 130
Die Lösung
Wenn man diese beiden Gleichungen addiert, fallen C und U automatisch weg:
(T + C – U) + (T + U – C) = 170 + 130
2T = 300
T = 150
Die Höhe des Tisches
Der Tisch ist 150 cm hoch.
Warum dieses Rätsel Spaß macht
Diese Aufgabe zeigt gut, wie man mit einfachen Gleichungen Probleme lösen kann, die auf den ersten Blick nicht unmittelbar klar sind. Ohne komplizierte Mathematik lässt sich durch logisches Denken eine exakte Antwort finden. Das macht sie zu einer perfekten Kopfnuss für alle, die kleine, elegante Rätsel mögen.





